Lista de Exercícios - Métodos Computacionais da Física B
Leonardo G Brunnet
20. Julho 2017
1 - Faça um programa que simule a difusão de M caminhantes
aleatórios em um espaço unidimensional.
- Faça histogramas da distribuição espacial de
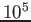 caminhantes
após 10000 passos quando esses se deslocarem respectivamente de
1,2 e 3 unidades de distância a cada passo de tempo.
caminhantes
após 10000 passos quando esses se deslocarem respectivamente de
1,2 e 3 unidades de distância a cada passo de tempo.
- Faça gráficos no gnuplot da distribuição espacial dos caminhantes.
- Ajuste o logaritmo (eixo y) dos histogramas encontrados a parábolas do tipo:
- Determine o desvio quadrático médio por passo em cada caso.
- Relacione o valor do parâmetro b ajustado com a distância percorrida
por passo e com o tempo.
2 - Use o método da transformada inversa para encontrar um gerador de
números aleatórios cuja distribuição, p(x), seja dada por
- Encontre a relação entre b e A que normaliza a distribuição.
- Determine os dois primeiros cumulantes dessa distribuição.
3 - Faça um programa que simule a difusão em uma dimensão de M
caminhantes de passos contínuos. A probabilidade de um passo de
tamanho 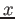 é dada por
é dada por
- Faça um histograma de distribuição de caminhantes, use
 .
.
4 - Refaça o problema anterior(3) usando o gerador encontrado no
problema 2. Use  .
.
5 - Use o método de Monte Carlo para calcular
onde 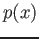 é definido na questão 2.
Use
é definido na questão 2.
Use  e a distribuição de números aleatórios é uma exponencial como
definida na questão 3.
e a distribuição de números aleatórios é uma exponencial como
definida na questão 3.
Leonardo Gregory Brunnet
2017-07-20
![]() é dada por
é dada por
![]() .
.