Lista Área 2 - Processos Estocásticos
Porto Alegre, 5 de dezembro de 2017
1 - A solução genérica para a equação de Langevin
pode ser obtida usando-se
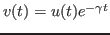 .
.
- Substitua para obter uma equação para
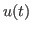 .
.
- Integre formalmente a equação para
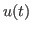 .
.
- Obtenha o valor médio para a velocidade.
- Obtenha o valor para o desvio quadrático médio da velocidade.
- Encontre o valor estacionário para esse desvio, calcule a energia cinética média e use o princípio equipartição de energia para encontrar a relação:
2 - O deslocamento quadrático médio pode ser obtido integrando-se a velocidade;
e usando-se a solução anterior para a velocidade;
3 - Distribuição de probabilidades da velocidade. Partindo da versão discretizada da equação de Langevin para a velocidade
(porque agora
 não é mais uma delta de Dirac?)
não é mais uma delta de Dirac?)
4 - Mostre que no limite de massa desprezível a equação de Langevin na forma discreta pode ser escrita como
5 - Use a forma encontrada no exercício anterior para escrever a equação de evolução de
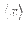 ,
,
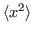 e
e
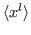 .
.
6 - Resolva a equação diferencial para a evolução de
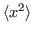 no caso de uma força restauradora:
no caso de uma força restauradora:
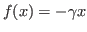 .
.
7 - Equação de Fokker-Planck (EFP).
- Partindo da equação de Langevin no limite de massa desprezível, relacione a função característica associada à
 com a função característica associada à
com a função característica associada à 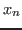 .
.
- Expanda as exponenciais até ordem
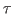 para obter
para obter
- Mostre que essa equação pode ser reescrita na forma
- Para encontrar a EFP faça a transformada inversa da equação obtida acima e tome o limite para
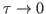 .
.
8 - Sob o ponto de vista da continuidade espaço-temporal da probabilidade, pode-se definir uma corrente de probabilidade 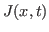 na EFP,
na EFP,
onde,
- Mostre que o fluxo de corrente nos limites
![$ [a,b]$](img35.png) do sistema deve ser idêntico para que a probabilidade fique corretamente normalizada.
do sistema deve ser idêntico para que a probabilidade fique corretamente normalizada.
- No caso de condições refletoras
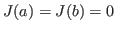 e no regime estacionário encontre a relação
e no regime estacionário encontre a relação
.
- Para o caso de uma força conservativa derivada de um potencial
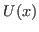 , mostre que
, mostre que
.
- Encontre a distribuição de probabilidades para o caso do potencial gravitacional próximo à superfície terrestre
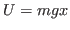 . Encontre o valor de
. Encontre o valor de 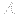 que normaliza corretamente a distribuição.
que normaliza corretamente a distribuição.
9 - Operador evolução: A EFP pode ser escrita na forma
sendo 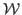 independente do tempo e tal que,
independente do tempo e tal que,
.
- Mostre que
- Por que pode-se usar
no caso estacionário? Note que isso também mostra que o autovalor nulo está associado à solução assintótica.
- Mostre que, formalmente, pode-se escrever a solução para a evolução da probabilidade como
- Supondo que
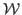 tenha um espectro discreto,
tenha um espectro discreto,
onde 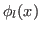 e
e  são, respectivamente, autofunções e autovalores de
são, respectivamente, autofunções e autovalores de 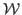 , pode-se escrever uma solução geral para a evolução de
, pode-se escrever uma solução geral para a evolução de 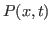 ,
,
Use os resultados dos ítens 1 e 2 desta questão para mostrar que a solução geral pode ser reescrita na forma
ou seja, que 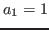 e
e  é a solução estacionária.
é a solução estacionária.
10 - Usando a definição de operador adjunto
para quaisquer 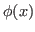 ,
, 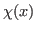 tais que
tais que
 , mostre que o operador
, mostre que o operador 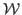 não é hermitiano pois
não é hermitiano pois
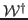 assume a forma
assume a forma
que é diferente de 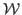 .
.
11 - Mostre que os autovalores de
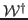 são os mesmos de
são os mesmos de 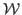 e as autofunções
e as autofunções 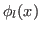 e
e 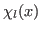 estão relacionadas por
estão relacionadas por
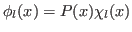 .
.
12 - Operador hermitiano. Define-se
onde
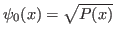 .
.
Leonardo Gregory Brunnet
2017-12-07
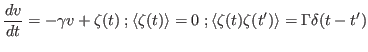

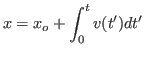
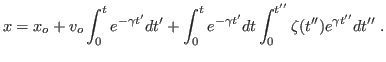
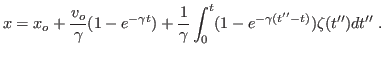
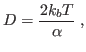
![]() ,
,
![]() e
e
![]() .
.
![]() no caso de uma força restauradora:
no caso de uma força restauradora:
![]() .
.
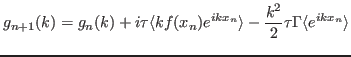
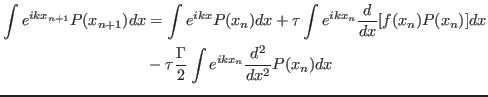
![]() na EFP,
na EFP, 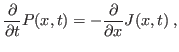
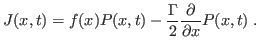
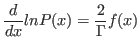
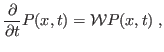
![$\displaystyle {\cal{W}}\phi(x)=-\frac{\partial}{\partial x}[f(x)\phi(x)] + \frac{\Gamma}{2} \frac{\partial^2}{\partial^2 x}\phi(x) $](img44.png)
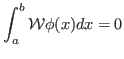
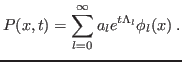
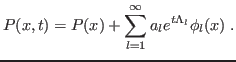
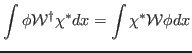
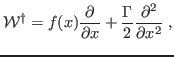
![]() são os mesmos de
são os mesmos de ![]() e as autofunções
e as autofunções ![]() e
e ![]() estão relacionadas por
estão relacionadas por
![]() .
.
